WP3. Seismic response simulation of industrial structures

Liquid storage tanks
To simulate the seismic response of liquid storage tanks (Figure 4a), rigorous finite element (FE) models will be developed, considering the actual tank geometry, material properties and imperfections. For horizontal-cylindrical and spherical liquid tank vessels, a systematic methodology will be developed, allowing the calculation of the total seismic force through modelling the hydrodynamic liquid-tank interaction. Furthermore, the deformable tank will be modelled with shell finite elements, which allow for: (i) Accurate consideration of liquid pressure on the tank wall and base plate. (ii) Simulation of the base plate and bottom tank support conditions (anchored or unanchored). (iii) Possible up-lifting of unanchored tanks. (iv) Inelastic behavior of steel material, including spatial variation of steel properties. (v) Simulation of tank roof, especially for the case of floating roof. (vi)Taking into consideration effects of tank nozzles and attached equipment. (vii) Inclusion of initial imperfections of the tank shell. 

The influence of imperfections (Figure 4b) in the structural response and capacity of industrial equipment structures has been observed experimentally and is considered responsible for the large variability in their response. For the needs of this project, actual field measurements will be used for the characterization of initial geometric imperfections and the degradation of the material properties in terms of deviations of the structures’ middle surfaces from their ideal perfect geometry as well as of spatial distributions of thickness, yield and ultimate materials stresses. These data will be extracted from case studies performed by the Research Team of the University of Thessaly. Specifically, the evolutionary power spectral density of the stochastic fields used for the description of initial geometric and material imperfections will be estimated using the method of separation (Schillinger & Papadopoulos 2010, Schillinger et al. 2010). 

For cases where measurements are not available, sensitivity stochastic analysis will be performed in order to identify critical values of the random parameters which are responsible for extreme values of the selected demand parameters (e.g. displacements or stresses). The solution of the stochastic finite element problem will be based on Monte Carlo Simulation together with efficient solution procedures that are able to reduce the computational effort by more than one order of magnitude. More specifically, preconditioned conjugate gradient methods will be applied, properly tailored to the solution of near-by problems with multiple right-hand sides, such as the stochastic problems under consideration, combined with efficient domain decomposition techniques and parallel processing procedures (Papadrakakis & Papadopoulos 1996, Papadrakakis & Fragakis 2001, Papadopoulos et al. 2009, Papadrakakis et al. 2011).

In addition to the above rigorous models, robust but efficient simplified models will also be developed. Simplified models take into account the main features of these structures and allow for their seismic performance estimation within acceptable limits of engineering accuracy (Malhorta et al. 2000). The simplified models will be used in the following WPs for the repeated non-linear and/or dynamic analyses in order to perform quickly the numerous analyses required for the seismic risk assessment, mainly based on an appropriate representation of liquid by a mass-spring model, and a simple procedure to calculate the compressive stress causing failure. The models will be verified using the results of the rigorous models of this WP.

Pressure vessels and piping systems
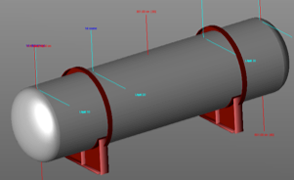
A similar approach will be used for the case of pressure vessels (Figure 5). Three geometries of pressure vessels will be considered: (a) spherical, (b) horizontal-cylindrical, and (c) vertical-cylindrical. Pressure vessels contain liquefied gas and their damage may lead to vessel-wall rupture with catastrophic consequences. For cases (a) and (b), there is no guidance on how to determine the hydrodynamic forces and therefore significant effort will be devoted on developing a simple and efficient methodology for accounting for these effects. Both rigorous and simplified models will be employed; the rigorous models will account for material and geometric nonlinearities, and allow for an accurate determination of stresses and deformations at critical areas, whereas the simplified models will be used for the repeated analyses of those systems.

Industrial piping systems, which are elongated structural systems supported on special steel structures called “pipe racks, form a unique type of industrial structural system of significant importance for the operation of the chemical or power plant (Figure 6). The simulation of piping will be conducted: (a) at a local level with rigorous finite element models in order to determine the strength of a piping component, and (b) at a global level with beam-type models to investigate the seismic behaviour of the piping and its support system. Piping components of critical importance are: pipe elbows or “bends”, i.e. flexible curved pipe segments, which are necessary for accommodating deformations due to variations of pressure and temperature, flanged or welded piping connections, which introduce discontinuities, leading to stress concentration and fracture and pipe nozzles at the locations where the pipe is connected to adjacent vessels and tanks and also at Tee piping junctions. These are locations where significant discontinuity occurs and potentially can lead to fracture under strong cyclic loading.

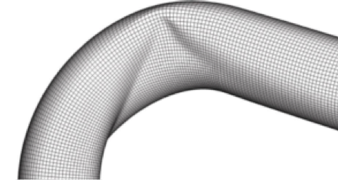
Apart from rigorous models, simplified models will also be developed and used for the analysis of piping systems, including the deformation of their supporting steel structure. The simplified models will take into consideration the nonlinearities of the piping components in a simple and efficient manner, and will be verified/calibrated from the results of the rigorous models (Touboul et al. 1999, Suzuki & Abe 2005). 

The research team of the University of Thessaly (UTh) will lead the numerical modelling of industrial equipment structures and the research Team of National Technical University of Athens (NTUA) will lead the stochastic modelling of initial imperfections. The Team Leaders and Team Members of UTh and NTUA have long experience and ongoing research on the aforementioned topics which guarantees the successful outcome of this WP (Karamanos et al. 2006a, 2006b, 2009, Varelis et al. 2011, Pappa et al. 2011, Diamanti 2011).

Key intermediate goals: Development of detailed and simplified Finite Element Models of liquid storage tanks, pressure vessels and pipes, calibration of simplified models, modelling of imperfections.